differential calculus

Limits

Sequences, functions, graphs

What do the numbers 1/1, 1/2, 1/3, 1/4, 1/5, . . . get closer and closer to? It may be clear that they approach zero, so we say the limit is 0.

The nth term is 1/n, so the notation is: lim (n -› ∞) 1/n = 0. (The -› means "approaches"; the ∞ is the infinity symbol.)

The same idea {using real numbers not just integers} is to consider the function f(x) = 1/x .
Then as x -› ∞ , f(x) -› 0 , so again we say lim (x -› ∞) f(x) = lim (x -› ∞) 1/x = 0. On the graph of f(x) we'd have a horizontal asymptote at y = 0, since the output values approach 0 as the graph goes off to the right. (click to review functions or graphing.)

Now what if x -› a and we try to see if f(x) approaches any specific value L. If it does, then we say that lim (x -› a) f(x) = L. (By definition x -› a means x is near a but not equal to a.)

Example 1:  Let f(x) = x + 3 . Then as x -› 3, f(x) -› 3 + 3, so lim (x -› 3) [x+3] = 6.

Example 2:  Let g(x) = (x^2 – 9) / (x – 3) . By algebra, we have

g(x) = (x + 3)(x – 3) / (x – 3) and if x ≠ 3 then we can cancel, so

g(x) = x + 3 if x ≠ 3. Notice that f(3) = 6 but g(3) is undefined.

The f(x) from example 1 has domain "all real numbers," and the g(x) from example 2 has domain "all reals except 3," so they're different functions. But the limit as x -› 3 is the same in both cases:
     lim (x -› 3) f(x) = lim (x -› 3) g(x) = 6.
Even though g(3) is undefined (it'd be 0/0), g(x) still has a limit (of 6), since x -› 3 implies x ≠ 3.

Example 3: Some other interesting limits:

a)   lim (x -› 0) [(sin x) / x] = 1

b)   lim (x -› 0) [(1 + x)^(1/x)] = e = 2.71828 approx

c)   lim (n -› ∞) [F(n+1) / F(n)] = (1 + √5) / 2 = 1.61805 approx. (The F(n) is the nth Fibonacci number of the sequence 1, 1, 2, 3, 5, 8, 13, . . .)

Differential Calculus

Tangent Lines & Derivatives, Differentiation Rules, Applications

Tangent Lines & Derivatives

On a straight line graph, y = mx + b, the slope is constant; it's equal to m no matter where you are on the graph. For the slope we figure (rise)/(run) = the same m at any point.
But on a parabola, like y = x^2, the direction keeps changing, so we'd expect that the "slope" doesn't stay constant. But how do you figure out the slope of a curve?

Example 1:  Think about the slope of a parabola.

The slope on the parabola y = x^2 is zero at the origin since the curve is horizontal there. At a different (x, y) location, what's the slope?

Let's take (3, 9) as an example; if we join up (3, 9) and a nearby point on the curve, say (3.1, 9.61), and compute "rise/run":  (draw yourself a picture)
     slope = (y2 – y1) / (x2 – x1) = (9.61 – 9) / (3.1 – 3) = 0.61 / 0.1 = 6.1

If we take a closer point (3.02, 3.02^2) = (3.02, 9.1204) then the slope is
     slope = (9.1204 – 9) / (3.02 – 3) = 0.1204 / 0.02 = 6.02

In fact for any h, the slope between (3, 9) and (3+h, (3+h)^2) will be
     slope = ((3+h)^2 – 9) / (3+h – 3) = (6h + h^2) / h = 6 + h

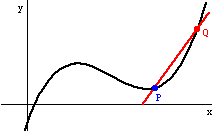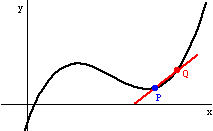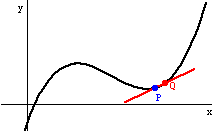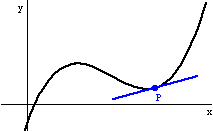
The line joining two points on a curve is called a secant line. The slope is msec. As h gets smaller and the points get closer together, the slope of the secant line approaches 6. The line it approaches is called the tangent line. The slope is mtan.

Here the parabola y = x^2 has a slope of 6 at (3, 9) because the limit (as h goes to 0) of 6 + h is 6.

Example 2:  What's the slope of any tangent line on the parabola?

Do the same thing at a general (x, y) point on y = f(x) = x^2:
Join up (x, x^2) and (x+h, (x+h)^2) and figure out the slope between them:
     slope = msec = ((x+h)^2 – x^2) / (x+h – x) = (2xh + h^2) / h = 2x + h.

As h goes to 0, this becomes mtan = 2x. The expression for "the slope at any x" is a new function, derived from f(x), called the derivative of f, and denoted f'(x).

Here we have: if f(x) = x^2 then f'(x) = 2x.
Checking this for our old point (3, 9) we see if x = 3 then f'(x) = 2x = 2(3) = 6. Ok!

Here's my cool Mathematica/QuickTime/GIFBuilder animation (from about 1995) showing the secant lines that approach the tangent line. The tangent line is the LIMIT of the secant lines, and the slope mtan is the limit of the slopes msec.

Note that the slope between P and Q "settles down" to a value mtan, which is the derivative of f at x, where x = x-coord of P.

Differentiation Rules!

Another notation for f'(x) is d/dx ( f(x) ). If y = f(x) then y' = f'(x) = d/dx (y) = dy/dx.
Notice from above we had d/dx (x^2) = 2x . What's the rule for the derivative of a power?
If we had f(x) = x^3 then f'(x) = ??? Let's use the limit definition of derivative:

d/dx (x^3) = lim (h -› 0) [( (x+h)^3 - x^3 ) / h ]
= lim (h -› 0) [ (x^3 + 3 x^2 h + 3 x h^2 + h^3 - x^3) / h ]
= lim (h -› 0) [(3 x^2 h + 3 x h^2 + h^3) / h]
= lim (h -› 0) [3 x^2 + 3 x h + h^2]
= 3 x^2 + 3 x(0) + 0^2
= 3 x^2

In general if f(x) = x^n (works for n = integer, fraction, or irrational!) then
Power Rule : d/dx (x^n) = n x^(n-1)
Sum Rule : d/dx [ f(x) + g(x) ] = d/dx f(x) + d/dx g(x) = f'(x) + g'(x)
Constant Multiple Rule : d/dx[ c f(x) ] = c d/dx f(x) = c f'(x).

Some special functions and their derivatives:
d/dx (sin x) = cos x , d/dx (cos x) = – sin x ,
d/dx (e^x) = e^x , d/dx (ln x) = 1 / x .

Example 1 :
d/dx (x^100) = 100 x^99 ;  d/dx (x^2 + 5 x) = 2 x + 5 ;
d/dx (√x ) = d/dx (x^(1/2)) = (1/2) x^(–1/2) = 1 / ( 2√x ) ;
d/dx (5 sin x – 3 cos x) = 5 cos x + 3 sin x.

We might have a product or quotient of functions:

Product Rule : d/dx [f(x) g(x)] = f(x) d/dx g(x) + g(x) d/dx f(x) = f(x) g'(x) + g(x) f'(x)
Quotient Rule : d/dx [f(x) / g(x)] = [g(x) d/dx f(x) – f(x) d/dx g(x)] /[g(x)^2] = [g(x) f'(x) – f(x) g'(x)] / [g(x)^2]

Here's what you do with a composition of functions:

Chain Rule : d/dx (f(g(x)) = f'(g(x)) d/dx (g(x)) = f'(g(x)) g'(x)
 
Example 2 :
d/dx (sin(3x)) = cos(3x) d/dx (3x) = 3 cos(3x)
d/dx (sin^3(x)) = d/dx [(sin x)^3] = 3 [ (sin x)^2 ] d/dx (sin x) = 3 sin^2 x cos x

Applications of Derivatives

Related Rates ,  Max-Min Problems

Related Rates

You guessed it -- define some variables, try to relate their rates (of change); we get a relation between their derivatives; technically known as a "differential equation."

Example:

Spoze you blow 30 cu.in. of air per second into a spherical balloon. How fast is the radius increasing when the balloon is 6 inches in diameter?

Solution: Ask the important questions:
* What are the variables involved?  V = volume, r = radius, D = diameter, t = time.

** What's the relation among them?  V = (4/3) π r^3; the volume formula for a sphere.
(There are lots of area and volume formulas)

*** Now take derivatives with respect to time t: (ok, that's not a question)
d/dt [V] = d/dt [(4/3) π r^3] = (4/3) π d/dt [r^3] ;
dV/dt = (4/3) π r^3 * 3 r^2 dr/dt = 4 π r^2 dr/dt ; this is the chain rule.

**** Then plug in what you know: D = 6 ==> r = 3, set dV/dt = 30 :
30 = 4 π (3^2) dr/dt ; solve for what you wanna know:
dr/dt = 30/(36 π) ≈ 0.265 in/sec.

Max/Min Problems

The philosophy here is to optimize some quantity Q that can depend on more than one thing (variable). Find a relation (constraint) and use it to get the Q in terms of one variable; then set the first derivative equal to zero and solve! (Oh, I was supposed to coax YOU into discovering all that.)

Example : Of all the rectangles of area A, which has the shortest diagonals?

Approach : Ok, use x = width, y = height; then xy = A; we want to minimize D = (x^2 + y^2) ;
we can sub in y = A/x since A is constant. Also we can minimize D^2 and D will be smallest.
D^2 = x^2 + (A/x)^2 ; now it's in terms of one variable; take the derivative w.r.t. x :
d/dx (D^2) = d/dx (x^2 + (A/x)^2) =d/dx(x^2 + (A^2) x^(-2))
= 2x + A^2 (–2 x^(-3)) = 2x – (2 A^2)/(x^3) =set= 0 ;
2x = 2 A^2 / x^3 ; x^4 = A^2 ; x = √A ; y = A/x = √A ;
Analysis : The best rectangle's a square, Captain Kirk.

back to lessons