dan's trigonometry lesson
©1997-2016 - all rights reserved - dan bach @dansmath
Similar Triangles and the Basic Six Trig Functions
The word "similar" means the same shape, but maybe not the same size. Like a scale model. What we need here is "proportionality." That's where CPSTP comes from:
Corresponding Parts of Similar Triangles are Proportional.
We use this similarity proportion to prove that in a right triangle, the ratio of, say, the height to the base depends only on the shape of the triangle and not the size of it.
So that means b / a = y / x , and we can define the tangent of the angle t to be any b / a :
tan(t) = b / a.
"Similarly" we define the sine and cosine functions:
sin(t) = b / c and cos(t) = a / c.
There are also the reciprocal functions:
cot(t) = 1 / tan(t) = a / b , sec(t) = 1 / cos(t) = c / a , and csc(t) = 1 / sin(t) = c / b .
Solving Right Triangles
When I got my teaching job at DVC (back in the 20th century), my dad asked me what I was teaching.
I told him "Calculus, Statistics, and Trig."
He replied, "Trigonometry? Oh, I learned that. Isn't it stuff like, you're 100 feet from a building, how tall is the building?"
I said you might need to know some more information, Dad, like maybe an angle.
In the little story, my dad also needed to know either:
1 ) the distance c from himself to the top of the building, or
2 ) the angle t from the horizontal up to the top of the building.
Let's look at each case:
(1) You might know about the Pythagorean Theorem, which relates the three sides of a right triangle:
a^2 + b^2 = c^2.
Click here (soon) for a cool picture proof of this theorem!
If we know the distances a and c, then in this case we can just use algebra to find the height, b.
For example, if a = 100 ft and c = 120 ft, then using b^2 = c^2 – a^2,
b = -/(14400 – 10000) = -/4400 ≈ 66 ft 4 in.
(2) If we know the angle of elevation t , then we can use the appropriate trig function to find the height. Since we know the horizontal distance a = 100 and we want the height b, we use the function that relates these: the tangent function: tan(t) = height / horiz = b/a .
So if the angle is maybe 40 degrees, then the height is given by
tan(40°) = b/a = b/100 , so b = 100 tan(40°) ≈ 83 ft 11 in.
Circles, Angles, Radians
How high off the ground are you, and how far have you gone, if you're in a Ferris Wheel (like a giant bicycle wheel with people in it) in which the people at the top are 50 feet off the ground, and you've gone 3/8 of the way around?
You could draw a picture and measure, but let's figure out the angle and use trig. The angle all the way around is 360° (that means degrees for now), so 3/8 of that is 135°, figure out the sine of 135° (it's -/2 / 2, think about it) and add 25 of those to the 25-ft radius, and get
h = 25 + 25 -/2 ≈ 42.7 ft off the ground.
But how far have you traveled? That's an arclength question; it's 3/8 of the circumference of a 25-ft radius circle; so: s = (3/8)(2π)(25) = 75 π / 4 ≈ 58.9 ft.
Notice that the angle itself can be given in terms of the arclength compared to the radius; "all the way around" the circle is 2π radius lengths, so the angle 360° is called 2π radians.
One radian = 360°/(2π) = 180°/π , or about 57.3 degrees.
Solving General Triangles, Law of Sines and Cosines
Ever wonder why, in any triangle, that the longest side is always opposite the biggest angle? There's a way to make it more exact, called the Law of Sines:
In a triangle ABC, with angles A, B, C opposite sides of lengths a, b, and c :
(sin A) / a = (sin B) / b = (sin C) / c (Show me the proof!)
Also, what about the third side of a triangle if you know two sides and the included angle? If the angle were 90 degrees you could use the Pythagorean Theorem, but in general there's the Law of Cosines:
In a triangle ABC, with angles A, B, C opposite sides of lengths a, b, and c :
c^2 = a^2 + b^2 – 2ab cos C . (Show animation!)
This is cool because if C is a right angle, then cos C = 0 and we get the good old Pythagorean Theorem.
Graphs of Trig Functions
(using Mathematica for pictures)
Linear equations like y = mx + b give lines, and quadratic equations, y = ax^2 + bx + c, give parabolas, but the trig functions sine and cosine give waves (like a side view of a slinky) that go on forever.
This sine wave animated GIF has been running continuously since 1997!
sine function Here's a cool sine animation (I did it in 1996, Mathematica to QuickTime to GIFBuilder); the height of the "stick" is the sine of the angle; the green length is the angle in radians, from 0 to 2π.
This is like a vibrating guitar string held in the middle.
amplitude
The above animated graph showed the function y = sin(x), which is y = 1 sin(x).
The following animation shows y = A sin(x) , for A = -3, -2, -1, 0, 1, 2, and 3.
You can see the effect the amplitude A has. In sound waves this is the 'volume'.
More like a compressed spring than a vibrating string.
frequency
On the other hand, y = sin(x) is y = sin(1 x).
The graphs of y = sin(B x) all have amplitude 1 but differ in frequency.
Notice the graph of y = sin(x) has period P = 2π = one 'wavelength.'
The bigger the B, the less x has to vary to do sin(2π) , and so the period of y = sin(Bx) is 2π/B ; in sound the frequency is 'pitch' or which note it is. Here's an animation showing this springy phenomenon.
phase shift & horizontal shift
The horizontal position of the graph is controlled by the B and the C in the equation y = sin(Bx – C).
The B is the frequency (see above), and the C is the angle or phase and affects the wave horizontally.
If B = 1, then y = sin(x – C) is just y = sin(x) moved to the right by C. This is because if x = C then we're doing sin(0).
For general B, write y = sin[B{x – (C/B)}]. Then if x = C/B we have sin(0). So it's a horizontal shift to the right by C/B.
The equation y = sin(2x – π/2) would have period π, phase shift π/2, but horizontal shift of only π/4. So y = 0 when x = π/4.
Polar Coordinates
In navigating a ship, you wouldn't hear the cry, "there's an iceberg 3 miles east and 4 miles north of us!", you'd hear "there's an iceberg 5 miles away, at a heading of about 53 degrees north of east!" The radar screen is set up to give angles and radial distances, not x and y coordinates.
We call the radial distance r and the angle of elevation t (for the Greek letter "theta.") The pair of numbers (r, t) form the polar coordinates of the point. See the picture for the simple relation between (r, t) and (x, y).
By definition, cos t = x / r and sin t = y / r , so x = r cos t and y = r sin t
Graphs in Polar Coordinates
The use of polar coordinates can create some cool-looking graphs; shapes like circles and petal curves, limaçons, and spirals have very complicated equations in rectangular coordinates (x, y), but much simpler, more elegant relations in polar (r, t).
Here are a few examples; I encourage you to try your own using a graphing calculator or computer. There is free graphing software online; here are a few apps/sites to try:
www.desmos.com (very popular, can browse and save activities)
www.geogebra.org (has 3D graphing capabilities)
www.graphcalc.com (pretty old, 2003 latest update)
These polar graphs were done (by me in 1999) in Mathematica:
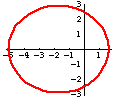
circle
r = 3
cardioid
r = 2 + 2 cos t
limaçon
r = 1 + 3 cos t
spiral
r = t / 5
petal curve odd
r = 4 cos 3t
petal curve even
r = 3 cos 2t
ellipse
r = 5 / (2 + cos t)
bach's bug
r = 2 cos 3t + 2 sin 4t