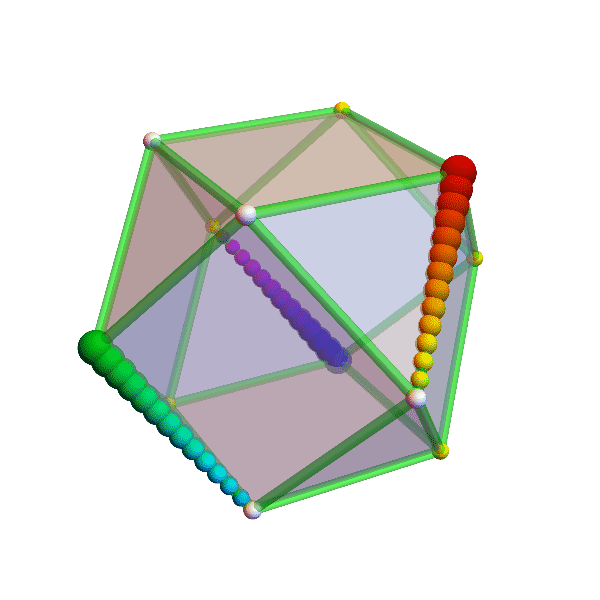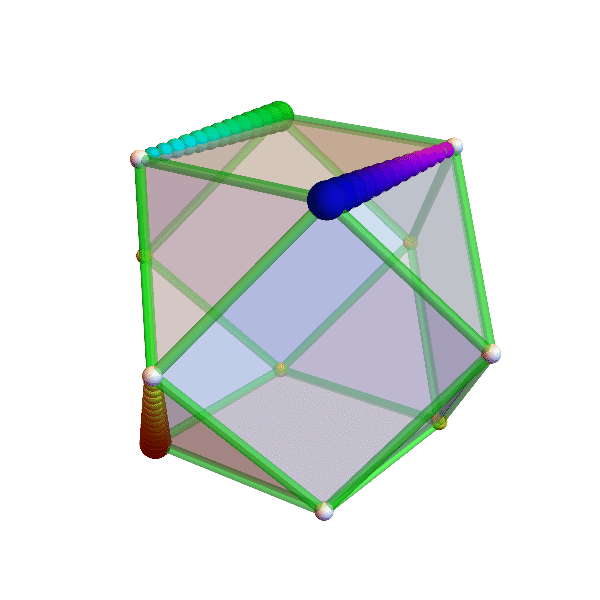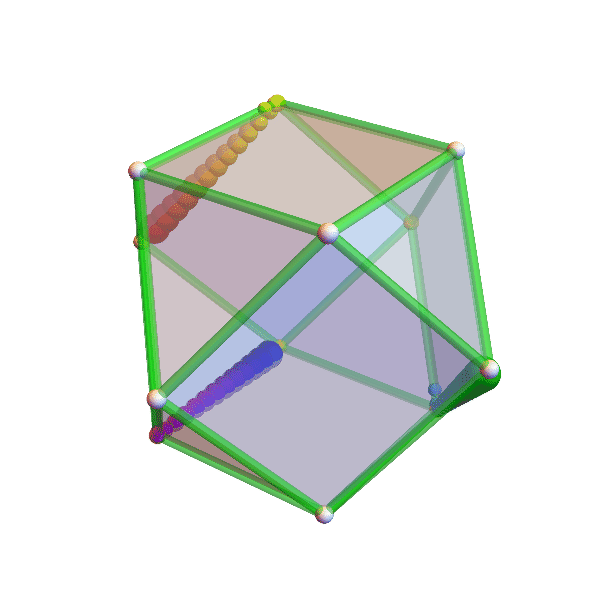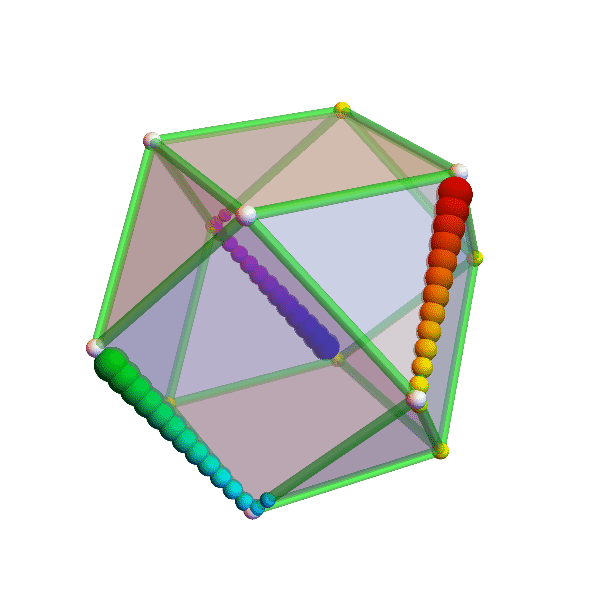
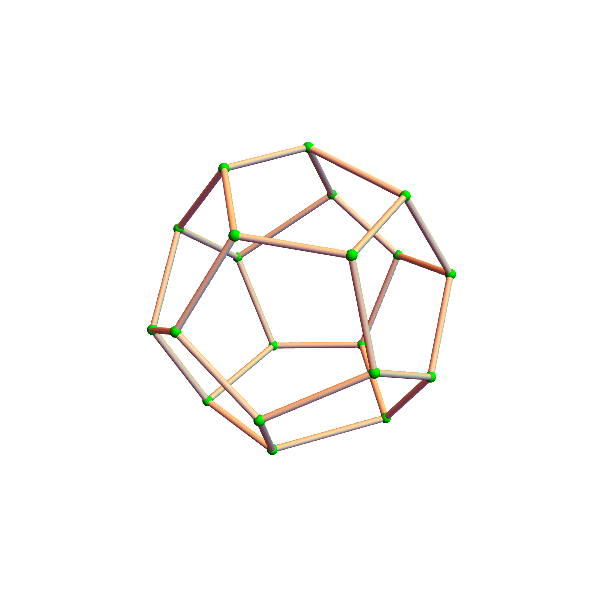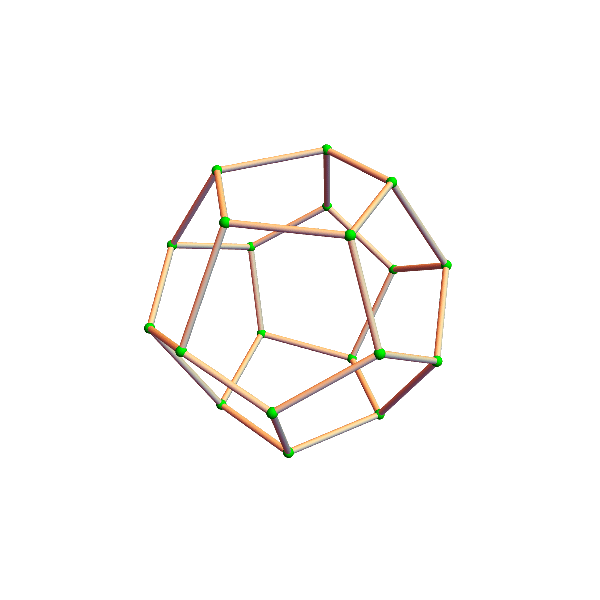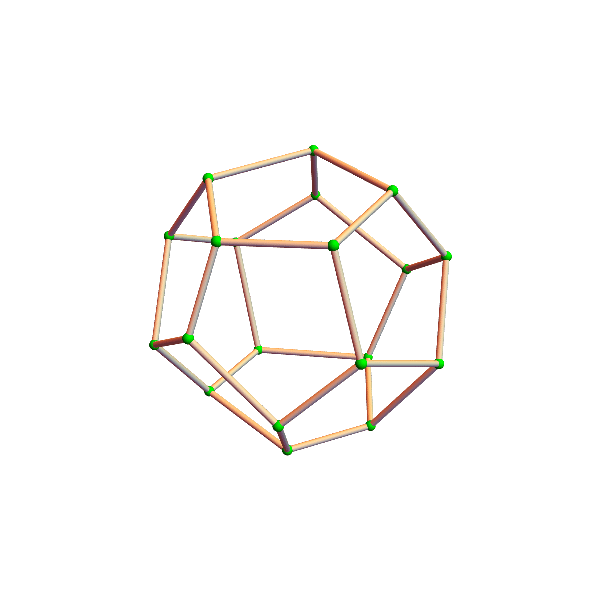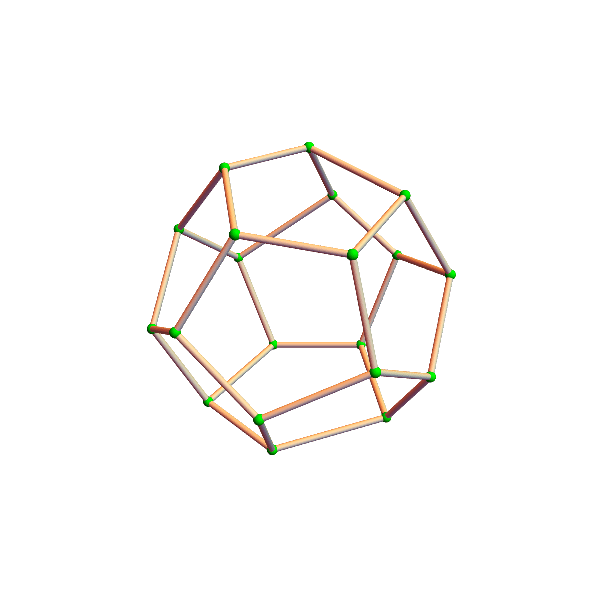
crooked cubes
the eight vertices (corners) of a cube wander around their assigned position, changing the square faces into trapezoids and rectangles. the official unit cube (pink) sits there, unperturbed, while the crazy crooked (green) cube intersects with it, and other surprises ensue. can you figure out whether the volume of the crooked cube is changing?